Adding harmonic distortion with Arduino Teensy
This guide is complete, but I’ve since written a concise four-step guide to achieve the same thing, based on Chebyshev polynomials, along with more discussion about harmonic distortion.
A couple of months ago, I picked up a Teensy 4.0 and the Audio Adapter Board because I wanted a cheap but simple platform for trying DSP on my music. One of the things I lately wanted to try was adding harmonic distortion, especially since it usually gets the credit for the sound of tube amplifiers. To accomplish this, I did some calculations, and I found out that I could apply any harmonic distortion profile I wanted (with a caveat). The key was using the Teensy Audio library’s “waveshape” block, a module that can map the value of a sample to another value in an arbitrary fashion—as specified by a lookup table.
I posted my code on Github. Essentially, it takes in one factor for each harmonic order, and this factor is the maximum ratio between the fundamental and the harmonic amplitudes, achieved if the fundamental swings over the entire digital range. Otherwise, the real ratio will be smaller, but real tube amplifiers also behave like this.
Results
I’ll lead with the results. I tested the code for putting in a second harmonic with a ratio of 0.05 and the third harmonic with a ratio of 0.005, measuring what went in and out.
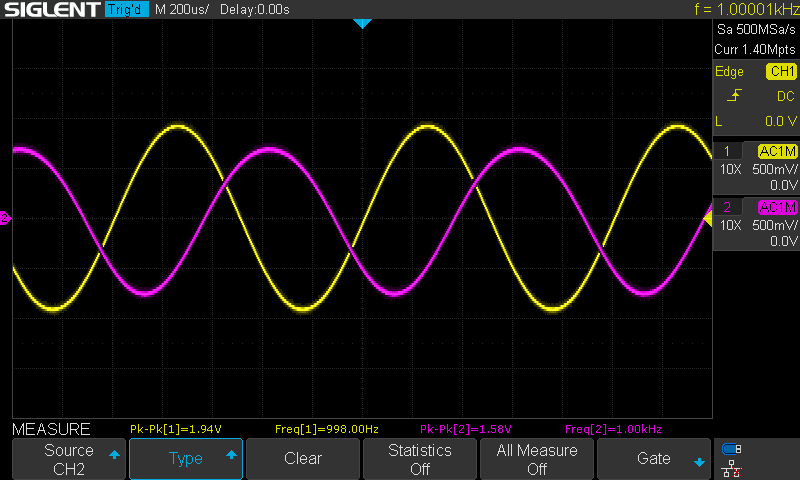
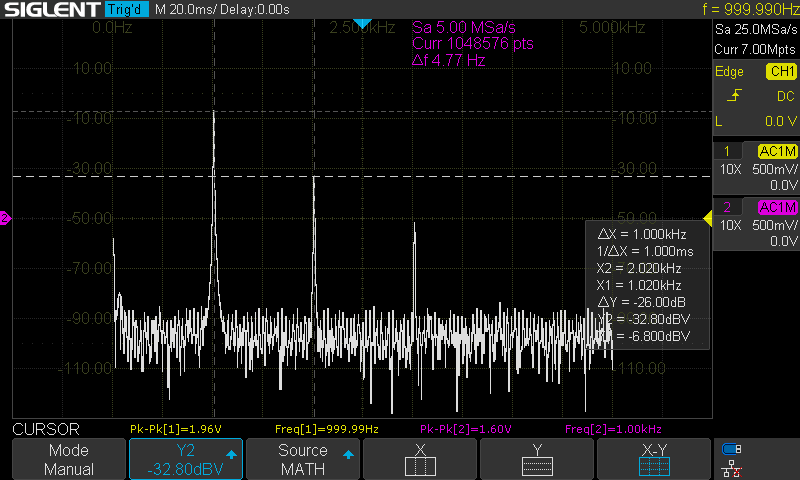
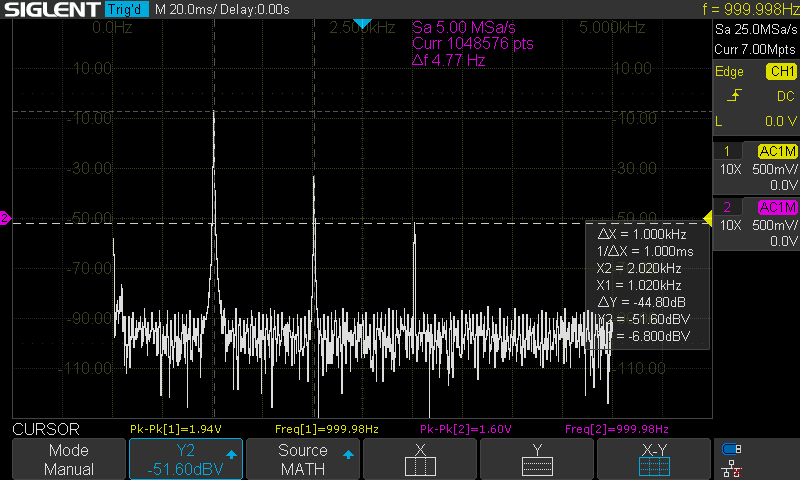
I initially measured this with a cheap DSO138, but it was introducing artifacts that wouldn’t let me see clearly beyond the second harmonic. However, measuring this with a proper oscilloscope showed that the Teensy got it spot-on.
Listening to it, I can agree with the people saying that harmonic distortion adds a little more body to the music. That was more clear when I felt a little something was missing as I switched it off. But I struggled to pick it out, even with a ratio of 0.05 (equivalent to a <=5% THD)! Anyway, this could explain why people gravitate toward the Darkvoice 336SE, which claims a THD of <2%.
Calculations
Beginning with a pure sine wave represented by the function $f(x) = \sin(x)$, we can add second harmonics by adding a $\sin(2x)$ term. This gives us $f_1(x)=\sin(x)+\alpha \sin(2x)$ where alpha represents the ratio between the second harmonic and the fundamental. In fact, if this harmonic is all we add, $\alpha$ is exactly the THD.
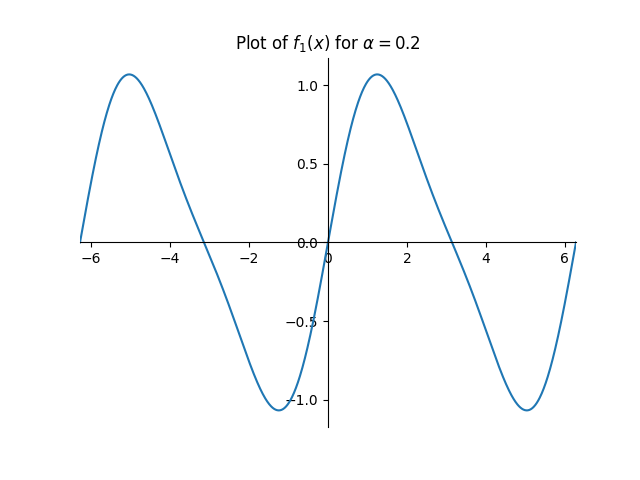
However, this alone is actually a challenge to generate in real time. Where a point on the original curve maps to ends up depending on the phase $x$ on the original sine wave. Yet why is the phase needed?
Taking just the value $y = f(x)$ instead, there are two possible phases in a given cycle, $x_1$ and $x_2$, that produce it. Because $f_1(x)$ has two different outputs for $x_1$ and $x_2$, knowing $y$ alone does not give which output it maps to.
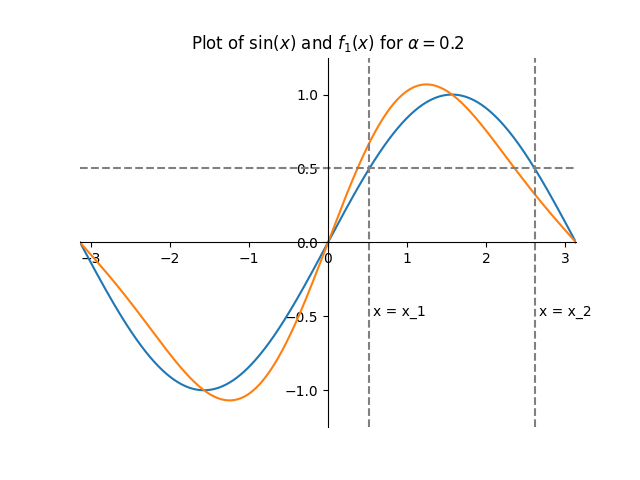
Really though, there is no obvious way to acquire $x$. Instead, mapping value to value, $y$ to $y_\text{new}$, is exactly what the Teensy Audio waveshaper can do. So, this whole harmonic distortion trick can be implemented just if $f_1(x)$ outputted the same for $x_1$ and $x_2$, allowing us to ignore the question of which $x$. In this example, we just need to shift the second harmonic by $-\frac{\pi}{2}$. This gives the function $f_2(x)=\sin(x)+\alpha \sin(2x-\frac{\pi}{2})$, and that is the one caveat we have to accept if we want to produce harmonic distortion this way.
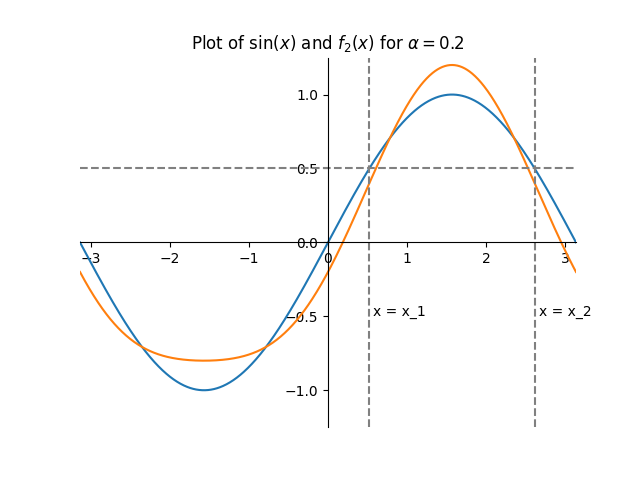
This can easily be generated with a waveshaper. However, there are a couple final steps before making this into a lookup table that we can use. First, right now we would be mapping the value zero to something nonzero, and this would introduce a constant DC offset to our signal! We can fix this by adding a constant term equal to $\alpha$, and so we’d use the function $f_2(x)=\sin(x)+\alpha \sin(2x-\frac{\pi}{2})+\alpha$ instead. Next, the Teensy Audio waveshaper does not accept mappings that are outside the range $[-1, 1]$. We can fix this by dividing the entire function $f_2(x)$ by the maximum absolute value it reaches, or in other words
\[f_{2, \text{maxabs}} = \max_x \lvert f_2(x) \rvert\]Yes, this is a normalization.
In practice, we can just find $f_{2, \text{maxabs}}$ by plotting it. In this specific case, it happens that $f_{2, \text{maxabs}} = 1+2 \alpha$.
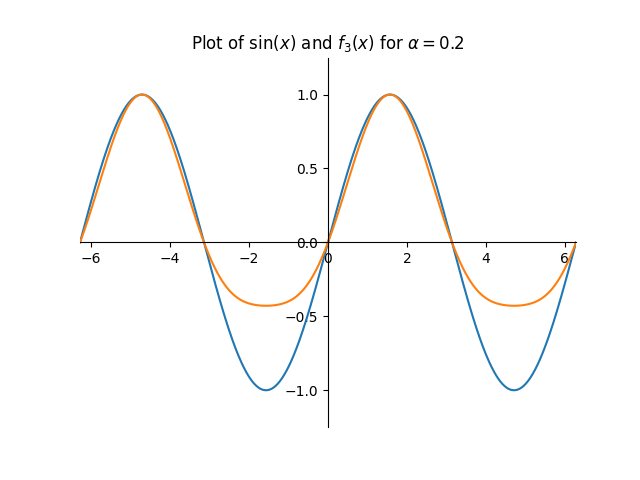
Our final function is $f_3(x)=\frac{f_2(x)}{f_{2, \text{maxabs}}}=\frac{\sin(x)+\alpha \sin(2x-\frac{\pi}{2})+\alpha}{1+2 \alpha}$.
This final function can easily be made into a lookup table—all we need to do is plug in $\sin^{-1}(y)$ for $x$. This way, we get a phase between $-\frac{\pi}{2}$ and $\frac{\pi}{2}$ for some value $y$ the lookup table is going to see. Then, we can get the single corresponding $y_{\text{new}} = f_3(x)$ because we can ignore that question regarding which of the two possible phases. The result, our lookup table is calculated with $y_{\text{new}} = f_3(\sin^{-1}(y))$ where $y$ is what the lookup table sees and $y_{\text{new}}$ is what the lookup table puts out.
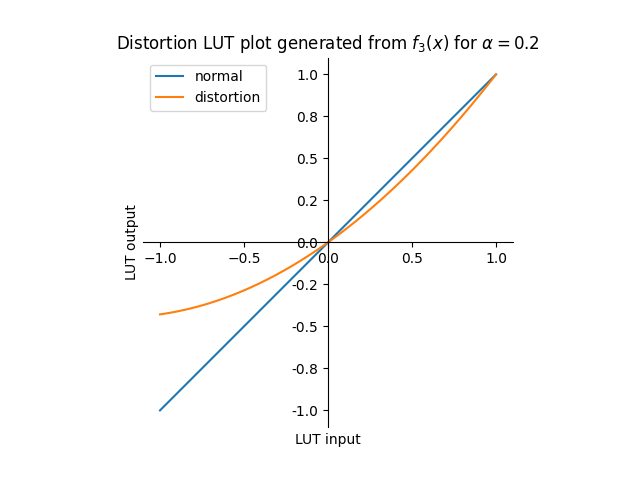
This process is possible for any desired harmonic or even any desired combination of harmonics. For each, the same logic shown here can be worked out from scratch. However, here are some pointers:
- A phase shift that works for the $n$-th harmonic is $-(n-1) \frac{\pi}{2}$
- Only even harmonics introduce a constant DC offset, and odd harmonics don’t
- Every other even (4th, 8th, etc) harmonic causes a DC offset in the opposite direction, and that can be compensated by adding $-\alpha$ instead
- When adding multiple harmonics, the only change is that the normalization happens after all the harmonics are added
For example, for a second harmonic with a factor of 0.1 and a third harmonic with a factor of 0.01, the final function should be $f_3(x)=\frac{\sin(x)+0.1 \sin(2x-\frac{\pi}{2})+0.1+0.01 \sin(3x-\pi)}{1.21}$ where $1.21$ was the maximum absolute value.